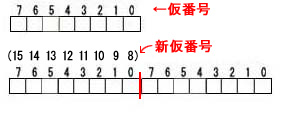
下図のような８ビット列(= １バイト)Boxや１６ビット列（= ２バイト）のBoxがコンピュータの中にたくさんつなげて埋め込んであって、 このビットに続けて電気信号「０」か「１」を送ることによって 、計算だけではなくそれ以外にもいろいろと出来るような気がしてきました。

実際に情報通信、文字や画像や音楽なども一定のルールで連続した「０」か「１」に変換することで表現できるのです。 こんなことをデジタル化というようです。

数直線 = 実数の図形化　（準備１）

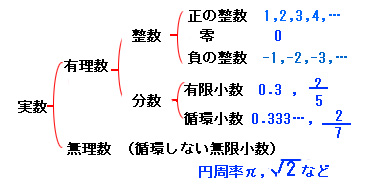
　世の中に実際に存在する数は「実数じっすう」と言います。大雑把（いい加減）な分類表を直ぐ下に描いてあります。 実際には存在しないけれども人間の頭脳（あたま）の中に作り上げた数は他にありますが、ここには触れません。
実数を図形化したものに「数直線」があります。
数直線の基本は原点Ｏ（オー）と、原点から右方に距離が「１」である単位点Ｅを有する向きを持った直線です。原点Ｏには０（零、ゼロ）、単位点Ｅには１を対応（目盛る）させ、座標と呼びます。Ｏ(0)，Ｅ(1) と表記します。原点Ｏから右方に距離がｐ（ｐ＞0）にある点Ｐについては、ＯＰ＝ｐ・OE の距離関係が成り立ちます。このようにして原点０の右側に正の数を対応させます（距離ですから）。また原点Ｏの左側に負の数を対応させる説明はあえて触れませんm(^_^)m　
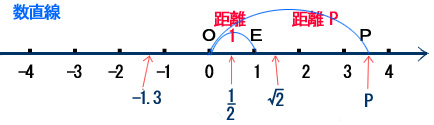
さて、このように定めた数直線には、実数が小さいものから大きいものへ右方向（→）に、順序良く、ベッタリと 埋めてあります。最初に述べたように、世の中に実在するすべての数が目盛られているわけです。
　あなたはこの数直線に（実数の並びに）隙間（すきま）があると思いますか 。興味のある方はデデキントの切断（せつだん）と呼ぶ物騒（おっかない）なものをホームページなどで検索してみてください。
よく知られている有理数について言えば、無数にギューツと埋まっていますが、隙間（すきま）だらけです。
何気なく「数」と呼んでいる実数は、普段は１０進数 で表記しているものです。

ここでは、うっかり罠（わな）を案内しましょう。
　足（た）し算して減る場合がたくさんある。例えば　４に「−１」を足すと３になる。　４＋（−１）＝３
かけ算して減（へ）る場合がたくさんある。例えば　４に「０．５」を掛けると２になる。　４×０．５＝２
負の数（−１）や小数（ 0. 5 ）などは気をつけなければいけません。分数の扱いもそうです。

グラフ = 点の集合体　（準備２）

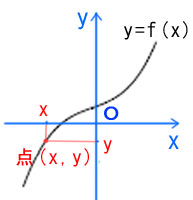
　直交（直角に交わる）する２本の数直線を 用いて座標平面を作る。デカルト（フランス）という数学者が考え出したものです。横に用いた数直線はｘ軸（右方が正）、縦の数直線はｙ軸（上方が正）といい、あわせて座標軸、その交点を原点Ｏ（オー）と呼びます。 この座標平面O-xy上に一定のルール（図を参考）で実数の順序組 （ｘ, ｙ）を点（ｘ, ｙ）と対応させる。そこに図形（＝グラフ）を描きます。実数 ｘ, ｙ の間の関係式：ｙ＝ｆ(ｘ）を満たすような点（ x ,y ）全体の 座標平面上の集合が、その関数ｙ＝ｆ(ｘ）のグラフと呼ばれるものです。

関数の考え方　（準備３）

　
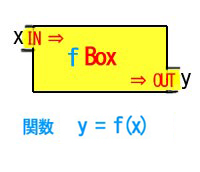
図は ｆ という名の Ｂｏｘ です。 左方の入り口（ＩＮ）に  x を１個入れると、 Ｂｏｘ の中でいろいろと加工（変化へんか）して、右方の出口（ＯＵＴ）から　 ｙ になって １個だけ出てきます。 ｘ, ｙは実数です。この 実数 x ⇒ 実数 ｙ が関数の基本です。（x ⇒ yであって、逆に y ⇒ xではありません。）
関数（かんすう）は、２つの変数（変化するもの） ｘ と y の間の関係を表すルール＝規則（きそく）で もあります。 ｘ を決（定）めると、その規則に従って y が１つだけ決（定）まるのです。このとき ｙ は x の関数であると言い y = f (x)　などと書きます。f は function の頭字です。　

指数関数　y = A^x　

関数（かんすう）については既に述べました

　Aは１でない正の数のとき、実数ｘ ⇒実数ｙの関係式 y = A^x を Aを底（てい）とする x の指数関数 （しすう）と言います。

ｙ＝２^ｘのグラフ （底Ａ=２ のとき）

ｘは実数の値ですから、 実数のところで述べましたが、ベッタリと連続して無数にあるのですが、 簡単にみるためにとびとびのｘの値（整数）について、ｙの値を計算し対応表に示しました。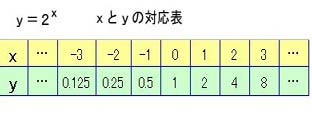
　
　次図は ｆ というＢｏｘ つまりは、関係式ｙ＝２^ｘを満たすような点（ x ,y ）全体の集合がそのグラフと呼ばれることに注意して、 順を追ってそのグラフを調べましょう。

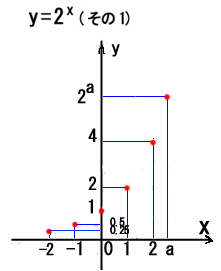
その（１）には対応表による　点（2, 4）、（1, 2）、（0, 1）、（−1, 0.5）などを座標平面に赤ポイントしてあります。
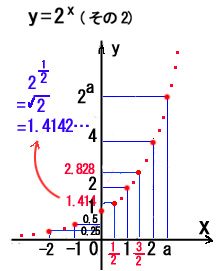
その（２）には、更に点（ , 1.414）、（ , 2.828）その他を追加してあります。 点の間の隙間が次第に詰ってきています。 どんどん点を書き加えてゆくとグラフが出来上がります。 大切なことは無数の点を集めると曲線になってゆきますが、 余程のことがない限り自然になめらかな曲線になるということです。実数の連続性という性質からついに最終のグラフは次に描いたような 連続した曲線になります。

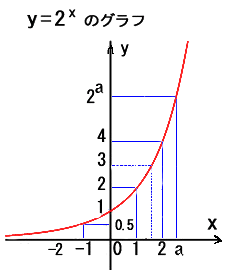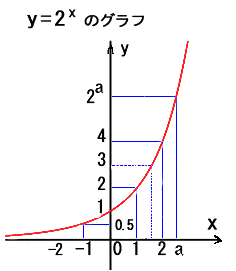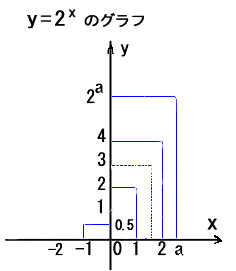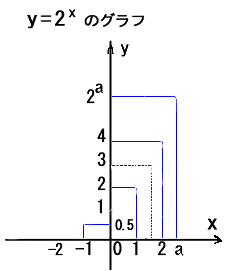
　Ａ=2 の場合、
　　指数関数　y = 2^x
 のグラフが完成しました。対応表（x の値に対するyの値）に基づき、点（a , ２^a）を幾つか書き入れています。
ｘ軸 より上方にあり、右上がりの滑稽（こっけい）なカーブです。
指数関数というのは小学生にはまだ早いと思いますから深入り無用です。また中学生程になると、図中で書いてない y = 3 となる　X の値を知りたくてウズウズすると思いますが、x = log₂ 3 （ロッグ）と知るのは「対数（たいすう）」が出てきてからです。　

指数法則をほんの少しだけ

Aは１でない正の数、 m, n は適当な数とする。
(1) A^m Aⁿ = A ^{m +n}
(2) A^m÷Aⁿ = A ^{m -n}
(3) (A ^m）ⁿ = A ^{m n}
(4)  Ａ^０ ＝ １
(5)
(6)
(4),(5),(6)は指数の拡張（かくちょう）<下に コメント入り>をするための大切な約束事です。これにより指数 ｍ, n がどんな数であっても成立することになっています。
A^m×Aⁿは  A^m・Aⁿ または A^m Aⁿと書いて　×記号を略する。乗算は加算より先に行う。 だからＡ＋ＢＣ　と（Ａ＋Ｂ）Ｃ　は異にする。

具体的にm , n　に数値を用いて法則を見てみよう。
例えば　
（１）について、m = 3,  n = 2 としてみると、
　A³A² = (AAA) (AA)　から
　A^３A^２ ＝ A^３＋２ ＝ A^５　は 成立が確かめられる。

（２）については、m = 5, n = 3  (m > n)  のとき
 A⁵÷A³ = A ^5-3 は より確かめられる。
　また（２）は、m = 3, n = 5  (m < n) のとき
 A³÷A⁵ = A ^3-5 は より確かめられる 。

（５）の約束は、負数の指数のために必要だったのです。

（３）について、例えば　(A²) ³=A ^2×3 について、
   A²A²A² = (AA) (AA) (AA) = A⁶で 確かめられる。

（６）は分数の指数への拡張（かくちょう）をする約束です。右辺は　ｎ乗したらＡ^ｍ　となる数で、累乗根（るいじょうこん）といいますが ここでは触れません。
 

１０進数のこと　⇒　１０を底とする指数関数 ｙ＝１０^ｘ

１０進数の基本は、１０を底とする指数関数です。

　上と同様に対応表を示しましたが、グラフは
特徴（形など）が ｙ＝２^ｘ　とほぼ同じになることが表から分かります。　
１０進数の構造（中身）について一般的に次のように考えます。
a_n-1 a_n-2 ……a₃ a₂ a₁ a₀ とn桁表示している１０進数を指数表現（１０が基数）すると
a_n-1・10^n-1 ＋a_n-2・10^n-2 ＋……＋a_3・10³ ＋a_2・ 10²_＋a_1・ 10¹＋a₀
例えば
　３２５＝３００ ＋ ２０ ＋ ５
　　　　＝３×１００ + ２×１０ ＋ ５×１
　　　　=３×１０^２ ＋ ２×１０^１ ＋ ５×１０^０ 
小数では
　３０．５４７＝３×１０^１＋５×１０^-１＋４×１０^-２＋７×１０^-３　　などです。

２進数（符号なし）を調べます

　ビット（bit）のポジションごとに、重み（ウエイトweight）= 位（くらいposition）を持たせます。雑な言い方をすると右方のビットは軽く、左方へゆく程に重い（偉い）。次表に具体例を示しました。 例えば仮の番号が３のビットは第４位（４けた目）にあり、 重みは２^３です。 ２^３の位（くらい）の数と呼びます。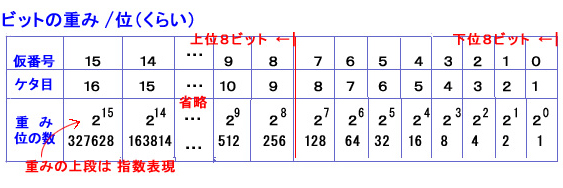

ほぼ準備が出来ました。

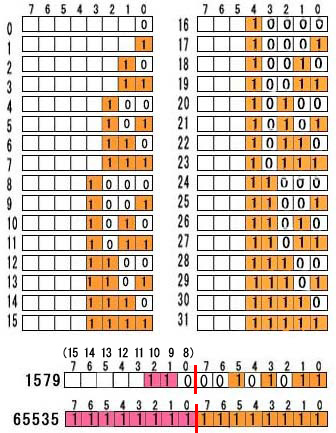
左図で例えば、ボックスナンバー13  は
２進数　1101 ですが、
1101= 1×2³ + 1×2²  + 1×2⁰
         = 8 + 4+ 1
         = 13 　(10進数の１３）
また適当に選んで
10111 = 1×2⁴+1×2²+1×2¹+1×2⁰
          =  16 + 4 + 2 + 1
          =  23_(10進)　
　これは、ボックスナンバー２３に一致しますよ。
 
左図は上表と較べるため、10進で 0 から 31 までの数について、８ビット（１バイト）Boxマシンの各ビットのスイッチの ON（1）、OFF（0） の様子を再掲示しました。

さらに、16ビットについて例を続けます。 16ビットの上図の方は
　110 0010 1011 ₍₂₎  = 1×2¹⁰ + 1×2⁹  + 1×2⁵ + 1×2³   + 1×2¹+1×2⁰ = 1579 ₍₁₀₎　→ 当然にボックスナンバーに一致ですネ。
また下図の方は
   1111 1111 1111 1111₍₂₎ = 65535₍₁₀₎  となることは各自で確かめて欲しいと思いますがボックスナンバー65535 にピッタシなのです。これが16ビットで表示出来る最大数です(符号なし整数)。
従って、2進数の構造（中身）について一般的にいうと次のようになります。 　a_△ は　0 か 1 のとき　
　a_n-1 a_n-2 ……a₃ a₂ a₁ a₀ と　n 桁表示している２進数を指数表現（２が基数）すると
a_n-1・2^n-1 ＋a_n-2・2^n-2 ＋……＋a_3・2³ ＋a_2・ 2²_＋a_1・ 2¹＋a₀

小数を今はチョットだけ扱います 　　

本格的には「分数 / 小数」ページで

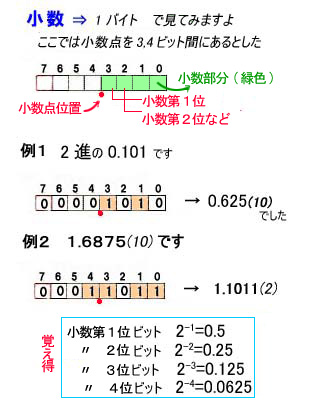
簡単のため、1バイト＝8ビットで見ます。
どこかに小数点があるものとします。どこでもいいんですが、今は3番ビットと4番ビットの間がその位置としますよ。

例１　1,3番ビットに電灯がつきました。
　3番ビット=小数第1位は、2^-1のケタ（重さ）
  1番ビット=小数第3位は、2^-3と考え、
  0.101 = 1×2^-1 +1×2^-3  
　　　　  = 0.5 + 0.125
  　　　  = 0.625₍₁₀₎となります。
例２
　1.1011 =1×2⁰+1×2^-1 +1×2^-3 +1×2 ^-4  
　　　= 1 + 0.5 + 0.125 + 0.0625
　　　= 1.6875₍₁₀₎  となります。

問題など

問１　次の２進数は、上図で表した場合にボックスナンバーはいくらになりますか。
（１） １０１ ０１１０　（2） １ １１１１ １１１１

問２　次の２進数を１０進数に直してみよう。 すべて正の数（符号なし）です。
（1） １１．０１１ （2）１０１．０１０１

問３　次の関数Ｂｏｘ のルールは何だろう！ 頭の体操m(^_^)m
 
(1)　１を入れると２が出てくる。２を入れると６が出てくる。３を入れたら１２が出る。４を入れたら２０が出てきます。
　さ〜てこの関数Ｂｏｘに５ を入れたら何が出てきますか。また　１０ を入れたら何が出てきますか。
 (2)　ｘ＝１のとき ｙ＝１。ｘ＝２のとき ｙ＝３。ｘ＝３のときｙ＝６。ｘ＝４のときｙ＝１０です。
　ｘ＝５のとき ｙはいくらですか。　また　ｘ＝１０のとき ｙはいくらですか。

• ホーム(index)
• 2進数とビット(bit)プロローグ
• 2進数と10進数の関係
• 10進数を2進数に変換
• 16進数
• 8進数とn進数(休憩室)
• 2進数の分数と小数
• 2進数の負数と補数
• AND OR XORなど
• 論理シフト演算
• 算術シフト演算
• 論理回路とゲート回路
• 2進数の浮動小数点
• 2進数のパズル
• 遊のゲスト掲示板