１０進数を２進数に変えよう

とにかく理由（わけ）が分からないと‥おもろくもない。

前ベージの答え

 問１ (2)　順に数えて、次の数が　10 0000 0000
　   =２ 9= 512 となると考えた方が早い。
 問２ (1）１１．０１１
　　＝1×21 +1×20 + 1×2-2 +1×2-3
　　＝２＋１＋ ０．２５ ＋ ０．１２５
　　= ３．３７５
補足です 、考えようではムダ足ですか。 
 問１　(１）86 (計算略します)
 　　　(２）511
 問２　(１)  3. 375
 　　　(２） 5. 3125 (計算略します)
問３　関数Ｂｏｘのルールの答え　
（１）３０、１１０　　
（２）１５、５５　
　（ここは２進数と関係はありません）

５５(10)　 を２進数に直す（方法その１）　　

あまり多用しませんけどm(*_*)m

５５＝３２＋１６＋４＋２＋１
　　＝２５＋２４＋２２＋２１＋２０
　　＝１×２５＋１×２４＋１×２２＋１×２１＋１×２０
　　＝１１０１１１（２） 当然のことながら、これは2進数を10進数に直す計算順序と逆なんですが。
マア、３２＝２５、６４＝２６　などが頭葉のどっかにあるからです。
　次に発想を変えて見ましょう！　シフトについては　論理シフト演算（1010ページ）に詳しく（くわしく）述べますから、 ここではチョット触れる程度です。
正の整数を扱っています。

１０進数→２進数について


仮に２進整数　C=cncn-1‥‥c3c2c1
に変わったとします。すべてのcmは0か１です。

Ｃを２で割る（をかけると同じ）と、１ビット右シフトと同じで
最下位ビットc1 が整数Boxから飛び出します。
（もし小数Boxが続いておれば、小数第１位ビットへ入る。）
　c1は０か１ですから、２で割ったときの余りです。
　c1=0 のとき元の数は偶数（割り切れる）
　C1=1のとき元の数は奇数です。 次に整数Boxに残った
　cncn-1‥‥c3c2 について、２で割ります。この最下位ビットc2が飛び出します。次々に繰り返します。最後に残りがcnになるまで続けます。
次はこれを使った計算方法です。

５５ (10)   を２進数に直す（方法その２）

これは良く使いますm(*_*)m

 
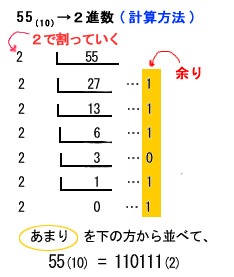
補足だそくに入りますヨ
2   |  32+16 +4 +2 +1
2   |  16  +8 +2 +1    余り　1
2   |   8   +4 +1         余り　1
2   |   4   +2              余り   1
2   |   2   +1              余り　0
2   |   1                      余り　1
         0                      余り　1

小数の１０進数→２進小数

かんたんにふれます。
詳しくは分数と小数（0111ページ)に書きます。　

例 ０．８１２５(10)  　を２進小数に


　この理屈も 楽しいので、 詳しい説明は 分数と小数のページに
　ゆずりました m(*_*)mです。
補足だそくに入りますヨ
0.8125× 2 = 1.6250
　整数（せいすう）部の１を取り（出して）
0.625 × 2 = 1.250
　整数部の１を取り
0.25 ×  2 =  0.5　　整数部は０　　　　　　　
0.5 ×2  =  1.0
　整数部の１を取り
残りが0 　＜0 になるまで続ける＞

問題で〜す　n(^_^)n

問１　１００００００（１０）　
　　を２進数に換えよう。
問２　０．４(１０)
　　を２進数に換えよう。 全て符号なし（正の数）です。
問１　この数は　百万です。
問２　困（こま）ったことに今度はピッタシと終わらない。
どこまでも続いて終わらないので、てきとうなところで終わってください。
現在では、ファイルサイズが何キロバイト、メモリー容量が何メガバイト、何ギガバイトのハードディスクなどと云います。 単純には、バイトマシンが、途方もなく多くつながっていると云うことです。

次に なぜ「約＝およそ」がつく？


　１キロバイトは
　１KB ＝ 約 １０００ バイト（B) です。
 　　（一休室にて説明しています） さらに　
　１メガバイト　１MB＝約１０００KB
　１ギガバイト  １GB＝約１０００MB
　１テラバイト　１ＴＢ＝約１０００ＧＢ
　‥‥　です。