分数/小数-２進数と遊ぶ(0111)

分数から小数（２進）へ

分数と小数

分数は小数の代役（かわり）が出来るだろうか。
分数と小数は本来異なったものでしょう。

は３分の１であって、0.333333… などでは意味がサッパリ分からなくなってしまうではありませんか。また、無限に 3 が続く（…で表している）厄介やっかいものにわざわざする必要もない。実はこれには「級数（きゅうすう）」という難しい話もついてくる。
前ページの「零の発見」で吉田先生は、分数は遠くエジプト、ギリシャが栄えた時代から知られていたものであり、小数はインド記数法（今の位取り記数法）が定着しつつあった１５世紀頃から出てくるのであると歴史的な事実を述べている。つまり全く違ったものなのです。

２進数の小数の中身の確認

小数の例はここに出しています。さて、
上のような数式表現は、小学生には無理があるかも知れません。指数の型にした場合は、さらに
　2^m・2ⁿ= 2^m+n
　(2^m)ⁿ= 2^mn　
など指数法則等にも触れないと意味が分かりにくく面白くありません。だけども深入りは必要ありません。

分母を見て、次のような分数の形だと小数に直すのはやさしい。

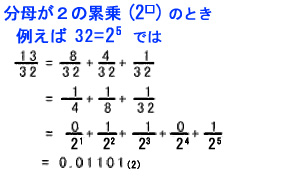
分母が２^□ （２の累乗（るいじょう））の形

　2¹, 2², 2³, 2⁴, 2⁵, 2⁶ , 2⁷,　…　　　つまり
　2,　4,　8,　16,　32,　64,　128,　… の分数の場合。

例　

　の分母はちょうどこの　32　である。
これは幾つかの分数の和（たし算）に持っていけば、２進小数の中身にまるまる一致させてしまうことが出来てしまう。なので
　_（１０） =　0.01101₍₂₎ですネ。

分数を２進小数になおす操作を理解するために

仮に２進小数に直ったと考えてみましょう。その小数部分Bは
　B = 0. b₁ b₂ b₃ b₄‥‥になったとします。　B の最上位ビット　b₁は、Ｂの２倍 ２×Ｂの整数部分にはみ出します。残りの b₂ b₃ b₄ ｂ₅‥‥は1ビットだけ左シフトします（左論理シフト）。

　これを繰り返すと　次々に b₂ b₃ b₄ ｂ_５‥　
が整数部分にはみ出してくれるということになります。

１０進分数を２進小数になおす

全ての１０進分数にあてはまります

例１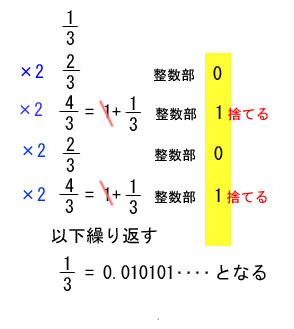　

を　２進小数になおします。

例２　を２進小数に直します。

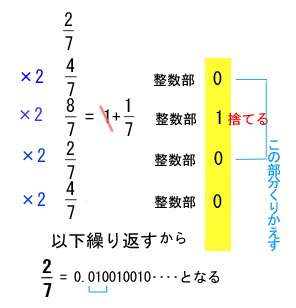
「捨てる」とは「とり出す」と言った方が分かりやすいかも知れません。また整数部分の０は捨てても捨てなくても、元の数に影響しないということから「捨てる」と書かないのです。
さて上の例は、分数をダイナミックに、２進小数に変えてみました。２倍することは、左シフトを１回行うことだから、次々にやっていくと、最上位（左端）から　１ビットずつ取り出せるということです。もちろん　１０進小数を２進小数に変えるときにもＯＫというものです。

ホント情報処理試験の問題です

問題１　 10 進数の分数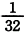

を 16 進数の小数で表したものは次のどれか。（平成２０年出題）
　　ア　0.01　イ　0.02　　ウ　0.05　エ　0.08

　　　答えは　【エ】です。
問題2　 16 進小数 0.C を 10 進小数に変換したものはどれか。（平成１９年出題）
　ア　0.12　　イ　0.55　　ウ　0.75　　エ　0.84 　

　　　　答えは　【ウ】です。

他の問題をやってみましょう。

１０進分数を　２進小数に換えてください。

問１

問２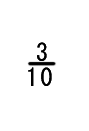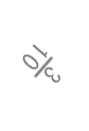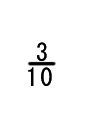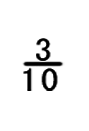

（註：問２　

は分母が　２^□ではない）

前ページ問題　の答え　

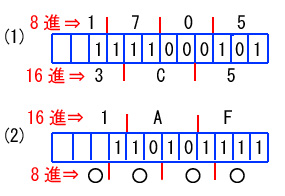
（１）上図より　1705₍₈₎は 3 C 5₍₁₆₎
2進表記した後は何ビット毎区切るかで明らか。
つまり
　(２) 16進の　1AF は　4ビットずつ区切って、
1/ 1 0 1 0 / 1 1 1 1
8進ではこれを3ビットずつ区切りなおして、
/1 1 0 /1 0 1/ 1 1 1⇒　6 5 7₍₈₎

（３）　200＝ 2×3⁴＋1×3³＋1×3²＋2　
のように基数３だから、重さ８１，２７、９、３を用いて分けて行く。答えは　２１１０２₍₃₎
（４）　３進数の３倍は１けた分の左シフトと同じ。１２０１⇒１２０１０
　　４倍は自分（１倍）＋３倍＝　１２０１＋１２０１０。３進数の足し算で　２０２１１を得る。
（５）　3進数で 1の位が 0となる数なので，3の倍数です。したがって、アまたはエとなります。
　次に、5進数で 1の位が 2となる 2けたの数は５で割ると余りが２であり、エは２ケタ内におさまらない。アが正解になります。
（６）７進数で計算したものです。
　少し調べてみましょう。
　ｎ進数とすると、
　　　202 = 2n²+2
54 = 5n+4
115 = n²+n+5 ですから
　202 - 54 = 115 　は、次のようになります。
　2n²+ 2　- ( 5n+4 ) = n²+n+ 5
これは２次方程式といいます。中学高学年からですが、無理して見てみよう。
　整理して　n²- 6n - 7 = 0
因数分解して　(n +1)(n -7) = 0
nは 6以上ですから n = 7 となります。
方程式を知らない小学生だったら、手っ取り早くいうと、
「シラミツブシ」手法で、
　6進数だったら‥
　7進数だったら‥
　8進数だったら‥
9進数だったら‥
A進数だったら‥
B進数だったら‥

と確かめていく覚悟をすれば、答えが出てくるでしょう。相当に投げやり（笑）
（６）別の考え方
　引き算が苦手なので、足し算でみると　115+ 54= 202 となります。
第１位だけを取り出して　5+ 4= [1] 2 となる筈です。（[1]は送られた１以下同様）
これが成り立つのは　7進法です。
次の位は　1+ 5+ [1]= [1] 0 でピッタシで
最上位も　1+ [1]= 2 ピッタシです。
（７)
割算が苦手なので、掛算でいきましょう。そうすると計算式は
131×5＝1015　となっています。虫食いの積み木で表すと次図です。

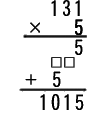
何進数でも 1×5＝5 ですから。
次に　3×5＝ □□　のところですが、
右側が１で、これがＮ進法だとすると、Ｎで割った余りが跳び出したものです。
10進で3×5=15 、7進の計算だと　2×7+1＝21
□□＝２１　でピッタシになります。　

２進数の分数と小数（0111ページ）